이분 탐색은 off-by-one error가 발생하기 쉬워서 늘 헷갈립니다.

이분 탐색 문제를 풀다보면 탈출 조건으로 lo <= hi, lo < hi, lo + 1 < hi 중 어느 걸 선택해야 할 지, 정답이 lo인지 hi인지 (lo + hi) / 2인지 모르겠고, 심지어는 while문이 끝나지 않아서 시간초과를 받기도 합니다.

이번 글에서는 이분 탐색을 헷갈리지 않게 구현하는 방법과 이분 탐색의 대표적 응용인 lower_bound, upper_bound에 대해 알아보겠습니다.

؜

1. [lo, hi]가 Check(lo) != Check(hi)가 되도록 구간을 설정

2. while (lo + 1 < hi)동안 mid = (lo + hi) / 2에서 Check(mid) = Check(lo)라면 lo = mid, 아니라면 hi = mid

3. 구한 경계에서 답이 lo인지 hi인지 생각해보고 출력

(1에서 경계는 항상 [lo, hi] 내에 존재하고, 2에서 Check(lo), Check(hi)는 변하지 않으며, 3에서 lo + 1 >= hi이고, lo < mid < hi에서 lo < hi이므로 lo + 1 == hi를 만족합니다)

؜

이분 탐색(Binary Search)은 결정 문제(Decision Problem)의 답이 이분적일 때 사용할 수 있는 탐색 기법입니다. 이때 결정 문제란 답이 Yes or No인 문제를 의미하며 (이분 탐색 문제에서는) 보통 1개의 parameter를 가집니다.

1 ~ 50까지 오름차순 정렬된 카드 더미에서 28번 카드를 찾는 문제를 예시로 이분 탐색을 알아보겠습니다. 편의상 첫 번째 카드부터 i번째 카드는 v[i], 28은 val로 표기하겠습니다.

이 경우 결정 문제를 "v[i] >= val인가?"로 잡으면 결정 문제의 답은 i가 증가함에 따라 F, F, ..., F, T, T, ..., T와 같이 분포함을 알 수 있습니다. 이때 우리가 찾고자 하는 값은 처음으로 v[i] >= val인 지점, 즉 처음 결정 문제가 True가 되는 i값입니다.

이렇게 결정 문제의 parameter(이 경우 i)에 대해 결정 문제의 답이 두 구간으로 나뉘는 것을 "이분적이다"라고 하며 이런 경우 이분 탐색을 사용해 결정 문제의 답이 달라지는 경계를 찾을 수 있습니다.

؜

이분 탐색의 아이디어는 경계를 포함하는 구간 [lo, hi]을 잡은 뒤 구간의 길이를 절반씩 줄여나가며 lo, hi이 경계 지점에 위치하도록 하는 것입니다. 이분 탐색이 끝난 뒤엔 lo의 다음 칸은 hi(즉, lo + 1 == hi)이며 Check(lo) != Check(hi)입니다. 이때 Check(x)는 결정 문제의 parameter가 x일 때 결정 문제의 답을 의미합니다.

위의 예시에선 [1, 50] -> [25, 50] -> ... -> [27, 28]로 lo, hi를 줄여나간 뒤 hi = 28을 찾아주면 됩니다. 이분 탐색은 구간의 범위가 클 때 특히 효과적입니다. 만약 카드가 100만장 있었다고 하면 특정 카드를 하나하나 앞에서부터 찾으면 최대 100만번의 연산이 필요하지만, 이분 탐색을 이용하면 2^20 >= 1,000,000이기 때문에 최대 20번의 연산으로 원하는 카드를 찾을 수 있습니다.

؜

+) 많은 최적화 문제는 이분 탐색으로 풀 수 있습니다. 최적화 문제란 어떤 조건(Check(x))을 만족하는 x의 최댓값 또는 최솟값을 찾는 문제를 말합니다. 이 경우 Check(x)가 x에 대해 이분적이면 이분 탐색을 사용할 수 있습니다.

؜

이분 탐색의 구현은 Check(lo) != Check(hi)가 되도록 lo, hi의 초기값을 잘 설정해준 뒤 lo + 1 < hi인 동안 mid = (lo + hi) / 2를 구해서 Check(lo) == Check(mid)라면 lo = mid를, Check(hi) == Check(mid)라면 hi = mid를 해주면 됩니다.

우선 초기 상태의 lo, hi가 Check(lo) != Check(hi)이기 때문에 결정 문제의 답이 바뀌는 경계는 [lo, hi] 내에 있음이 보장됩니다.

이제 lo + 1 < hi인 동안 [lo, hi]를 [lo, mid] 또는 [mid, hi]로 줄여나가는데, 이 경우 Check(lo), Check(hi)는 바뀌지 않습니다. 이유는 Check(lo) == Check(mid)라면 lo = mid를, Check(hi) == Check(mid)라면 hi = mid를 하기 때문입니다. 또한 lo + 1 < hi이기 때문에 lo와 hi의 사이에는 무조건 한 개 이상의 칸이 있으며, mid는 항상 lo < mid < hi를 만족합니다. 따라서 구간의 길이는 매번 절반씩 줄어들며 언젠간 lo + 1 == hi가 되어서 반복문을 탈출하게 됩니다.

(반복문을 탈출했다면 lo + 1 >= hi인데 lo < mid < hi인 mid를 대입하기 때문에 lo < hi이고, 두 조건을 만족하는 lo, hi는 lo + 1 == hi인 경우밖에 없습니다)

이분 탐색이 끝나면 lo, hi는 결정 문제의 답이 바뀌는 경계에 위치하게 되며, 만약 결정 문제 답의 분포가 F~T인데 정답이 가장 큰 F라면 lo를, 가장 작은 T라면 hi를 출력해주면 됩니다.

؜

1. 경계를 포함하도록, 즉 Check(lo) != Check(hi)가 되도록 [lo, hi]를 잡음

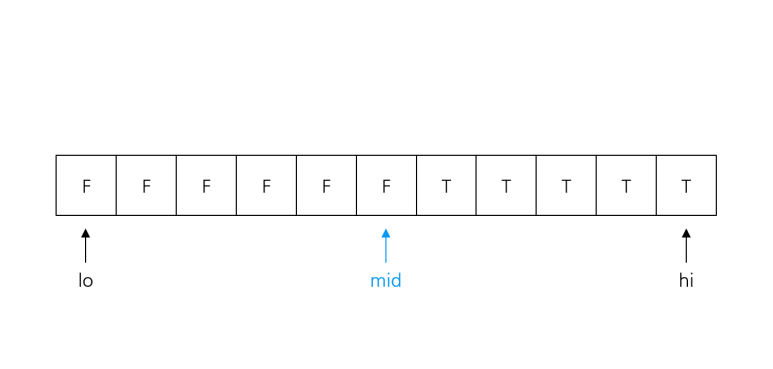
2. Check(lo) == Check(mid)라면 lo = mid, 아니라면 hi = mid를 반복

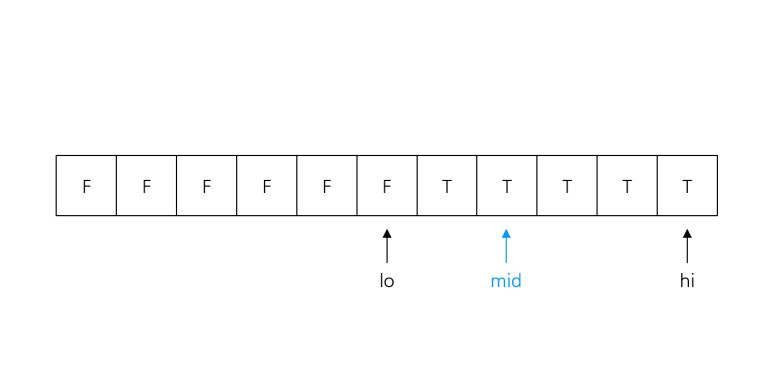
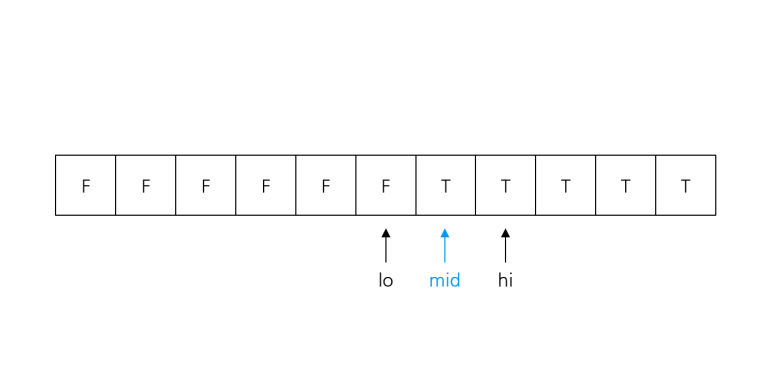
3. lo + 1 == hi가 되면 탈출, lo, hi는 경계에 위치

؜

예시로 나무 자르기(BOJ 2805) 문제를 보겠습니다.

결정 문제를 "mid 높이에 절단기를 위치했을 때 m 이상의 나무를 얻을 수 있는가?"로 잡아주면 Check(mid)의 분포가 T, ..., T, F, ..., F이고, 구하는 답은 Check(mid) = True인 mid의 최댓값입니다.

lo, hi의 초기값은 Check(lo) = T, Check(hi) = F가 되도록 lo = 0, hi = "가장 큰 나무의 높이"로 설정해주면 됩니다.

이제 bool을 반환하는 Check(mid)를 잘 작성하면 문제를 풀 수 있습니다. 이 문제는 mid 높이의 절단기로 각 나무를 모두 잘랐을 때 자른 나무의 길이가 m 이상인지 확인해주면 됩니다.

#include <bits/stdc++.h>
#define fastio cin.tie(0)->sync_with_stdio(0)
using namespace std;

int n, m, v[1'000'000];

// 결정 문제
bool Check(const int mid) { // mid 높이에 절단기를 위치했을 때 m 이상의 나무를 얻을 수 있는가?
    long long sum = 0; // 오버플로우 조심
    for (int i = 0; i < n; i++) {
        if (v[i] > mid) sum += v[i] - mid;
    }
    return sum >= m;
}

int main() {
    fastio;
    cin >> n >> m;
    for (int i = 0; i < n; i++) cin >> v[i];

    // 이분 탐색
    int lo = 0, hi = 1e9;
    // Checklist
    // 1. Check(lo) = T, Check(hi) = F를 만족하는가?
    // 2. lo는 정답이 될 수 있는 모든 범위를 나타낼 수 있는가? (정답은 0 ~ max(v) - 1라 가능)

    while (lo + 1 < hi) { // lo와 hi 사이에 다른 칸이 존재하는가?
        int mid = (lo + hi) / 2; // 항상 lo < mid < hi를 만족 (평균을 생각해보면 o)
        if (Check(mid)) lo = mid;
        else hi = mid;
    }
    cout << lo << '\n';
}

+) 이 문제처럼 결정 문제의 답은 항상 F~T 분포가 아니라 T~F 분포일 수도 있습니다. 또한 정답은 경계의 왼쪽(=lo)일 수도 있고 오른쪽(=hi)일 수도 있습니다. 따라서 결정 문제의 분포와 정답이 lo인지 hi인지는 문제별로 잘 생각해줘야 합니다.

؜

이분 탐색이 사용되는 대표적인 예시로 정렬된 배열에서 특정 값 이상 또는 초과인 원소가 등장하는 처음 위치를 찾는 문제가 있습니다. 이는 cpp를 기준으로 algorithm 헤더에 std::lower_bound, std::upper_bound라는 함수로 구현되어있습니다. 이번엔 이분 탐색으로 lower_bound, upper_bound를 직접 구현해보며 함수의 정의와 작동 원리를 알아보겠습니다.

먼저 lower_bound는 v[i - 1] < k <= v[i]인 i를 찾아주는 함수로, v[i] >= k인 i의 최솟값을 반환합니다. 만약 v의 모든 원소가 k보다 작다면 v의 마지막 다음 칸의 위치를 반환합니다.

upper_bound는 v[i - 1] <= k < v[i]인 i를 찾아주는 함수로 v[i] > k인 i의 최솟값을 반환합니다. 이 경우에도 v의 모든 원소가 k보다 작거나 같다면 v의 마지막 다음 칸의 위치를 반환합니다.

(개인적으로 '이상, '초과'라는 단어로 lower_bound, upper_bound의 정의를 기억하는 것보다 이렇게 식으로 정의를 기억하는게 더 명확하고 좋은 거 같습니다)

؜

예를 들어 n = 5, v = [1, 2, 3, 3, 4]일 때 lower_bound(v, v + n, 3)은 v[2] >= 3이기 때문에 2이고 upper_bound(v, v + n, 3)은 v[4] > 3이기 때문에 4입니다. 이때 upper_bound(v, v + n, x) - lower_bound(v, v + n, x)는 항상 v 내의 x의 개수를 나타낸다는 재밌는 성질이 있습니다. 이 식은 v 내에 x가 없다면 0이며, 있다면 x의 처음 등장 위치를 마지막 등장 위치의 다음 위치에서 빼는 것이기 때문에 항상 성립합니다. (단, v는 오름차순으로 정렬되어있어야 합니다)

(참고 : https://blog.naver.com/jinhan814/222549554931)

؜

lower_bound, upper_bound의 구현은 다음과 같습니다.

#include <bits/stdc++.h>
#define fastio cin.tie(0)->sync_with_stdio(0)
using namespace std;

int LowerBound(const vector<int>& v, int x) {
    const int n = v.size();
    int lo = -1, hi = n;
    while (lo + 1 < hi) {
        int mid = (lo + hi) / 2;
        if (!(v[mid] >= x)) lo = mid;
        else hi = mid;
    }
    return hi;
}

int UpperBound(const vector<int>& v, int x) {
    const int n = v.size();
    int lo = -1, hi = n;
    while (lo + 1 < hi) {
        int mid = (lo + hi) / 2;
        if (!(v[mid] > x)) lo = mid;
        else hi = mid;
    }
    return hi;
}

int main() {
    fastio;
    vector<int> v = { 1, 2, 3, 3, 4 };
    cout << LowerBound(v, 3) << '\n'; // 2
    cout << UpperBound(v, 3) << '\n'; // 4
    cout << UpperBound(v, 3) - LowerBound(v, 3) << '\n'; // 2
}

(hi는 v의 모든 원소가 k보다 작은(작거나 같은) 경우 n을 반환해야 하기 때문에 처음에 n이상으로 설정해야 합니다. 또한 hi는 최소 0까지 감소할 수 있어야 하기 때문에 lo = -1로 설정해야 합니다)

؜

Binary Search : https://www.acmicpc.net/workbook/view/9764

lower_bound, upper_bound : https://www.acmicpc.net/workbook/view/9264

؜

+) 2021-12-29 추가

개인 블로그에 연습 문제의 풀이를 추가했습니다.

1) https://blog.naver.com/jinhan814/222607789392

2) https://blog.naver.com/jinhan814/222549554931

؜

1. lo, hi는 항상 정답의 범위를 나타낼 수 있도록 해야합니다. 예를 들어 lo를 출력해야 하는 문제의 답이 최대 n일 때 hi = n으로 선언하거나, hi를 출력해야 하는 문제의 답이 최소 0일 때 lo = 0으로 선언하면 안됩니다. (hi = n + 1, lo = -1로 선언해야 합니다)

2. 오버플로우에 주의해야 합니다. 이분 탐색을 사용하는 문제는 대부분 수의 범위가 크기 때문에 오버플로우가 발생할 수 있습니다.

3. 결정 문제의 정의에 맞게 Check함수를 잘 구현해야 합니다. 예를 들어 lower_bound는 v[i] >= k인 i의 최솟값을 구하는 함수이고, upper_bound는 v[i] > k인 i의 최솟값을 구하는 함수인데, Check 함수의 부등호를 조금만 틀려도 전혀 엉뚱한 값이 튀어나올 수 있습니다.

؜

• 구종만, 「프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략」, 인사이트(2016), p128-132