가장 가까운 두 점 찾기 문제는 2차원 평면 위에 점 N개가 있을 때, 거리가 가장 가까운 두 점을 찾는 문제입니다. (2261번 문제: 가장 가까운 두 점)

N이 작은 경우에는 모든 경우를 다해보는 방식을 이용해서 구현할 수 있습니다.

#include <cstdio>
int x[100000];
int y[100000];
int dist(int x1, int y1, int x2, int y2) {
    return (x1-x2)*(x1-x2) + (y1-y2)*(y1-y2);
}
int main() {
    int n;
    scanf("%d",&n);
    for (int i=0; i<n; i++) {
        scanf("%d %d",&x[i],&y[i]);
    }
    int ans = -1;
    for (int i=0; i<n-1; i++) {
        for (int j=i+1; j<n; j++) {
            int d = dist(x[i],y[i],x[j],y[j]);
            if (ans == -1 || ans > d) {
                ans = d;
            }
        }
    }
    printf("%d\n",ans);
    return 0;
}

N이 10,000을 넘어가버리면, 모든 경우를 다해보는데 너무 오랜 시간이 걸리게 됩니다. 따라서 조금 효율적인 방법이 필요하게 됩니다.

가장 가까운 두 점은 분할 정복 알고리즘(Divide & Conquer)으로도 풀 수 있지만, 이 글에서는 Sweep line 알고리즘을 이용해서 구현해보겠습니다.

먼저, 점을 x좌표가 증가하는 순으로 정렬을 해놓아야 합니다. 그 다음 x좌표가 작은 것부터 하나씩 살펴봅니다.

알고리즘의 기본 아이디어는 다음과 같습니다.

1번 점부터 M-1번점이 있을 때, 가장 가까운 점의 거리를 구해놓았고, 그 거리를 d라고 합니다. 이제 M번째 점이 있을 때, 가장 가까운 두 점의 거리를 구해야 합니다.

가장 가까운 점의 거리가 d이기 때문에, M번점의 x좌표와 차이가 d이하인 점만 후보가 될 수 있습니다. 이 후보를 그림으로 나타내면 다음과 같습니다.

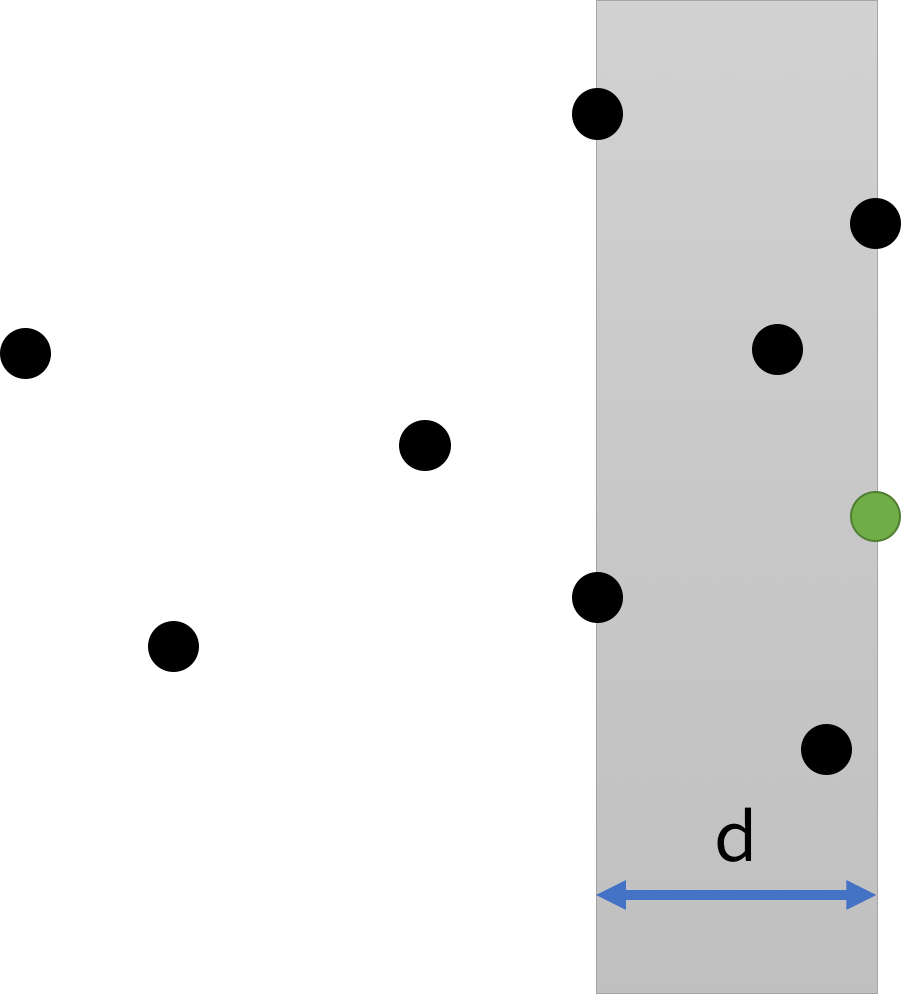
M번째 점과 회색 직사각형 안에 들어있는 점만 검사를 하는것으로 불필요한 검사를 줄일 수 있습니다.

#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
struct Point {
    int x, y;
};
bool cmp(const Point &u, const Point &v) {
    return u.x < v.x;
}
int dist(Point &p1, Point &p2) {
    return (p1.x-p2.x)*(p1.x-p2.x) + (p1.y-p2.y)*(p1.y-p2.y);
}
int main() {
    int n;
    scanf("%d",&n);
    vector<Point> a(n);
    for (int i=0; i<n; i++) {
        scanf("%d %d",&a[i].x,&a[i].y);
    }
    sort(a.begin(), a.end(), cmp);
    vector<Point> candidate = {a[0], a[1]};
    int ans = dist(a[0], a[1]);
    for (int i=2; i<n; i++) {
        Point now = a[i];
        for (auto it = candidate.begin(); it!=candidate.end(); ) {
            auto p = *it;
            int x = now.x - p.x;
            if (x*x > ans) {
                it = candidate.erase(it);
            } else {
                int d = dist(now, p);
                if (d < ans) {
                    ans = d;
                }
                it++;
            }
        }
        candidate.push_back(now);
    }
    printf("%d\n",ans);
    return 0;
}

배열 candidate는 그림에서 회색 직사각형에 해당하는 배열입니다.

항상 candidate에는 현재 점과 x좌표의 차이가 ans 이하인 점만 들어있게 됩니다. 그럼, candidate안에 들어있을 수 있는 점의 최대 개수는 몇 개 일까요?

바로 N개 입니다. 따라서, 이 방법은 매우 좋은 방법이지만, 시간복잡도는 모든 방법을 다 해보는 것과 똑같이 O(N^2)이 걸리게 됩니다. 조금 더 알고리즘을 개선시켜야겠네요.

여기서 x*x와 ans를 비교하는 이유는 ans에는 거리의 제곱이 저장되어 있기 때문입니다. 따라서, x좌표 차이의 제곱을 비교해야 올바른 비교를 할 수 있습니다.

생각해보면 회색 직사각형에서 M번점과의 y좌표 차이가 d 이하인 점만 거리가 d 이하가 될 수 있습니다.

회색 직사각형에서 y좌표가 d이하인 점만 찾아서 거리를 비교하면서 답을 갱신할 수 있습니다.

그럼, 어떻게 구현을 해야 할까요?

candidate 배열을 y좌표를 기준으로 정렬해서, 이분 탐색을 이용해 M번점과 거리 차이가 d인 점의 구간을 찾아서, 그 구간에 들어있는 점만 검사하는 것이 좋지 않을까요? 즉, candidate 배열에서 y좌표가 M의 y좌표 - d보다 큰 점 중에서 가장 인덱스가 작은 점과, M의 y좌표 + d보다 작은 점 중에서 가장 인덱스가 큰 점을 찾아야 합니다. 이 두가지는 lower_bound와 upper_bound를 이용해서 구할 수 있습니다.

#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
struct Point {
    int x, y;
    Point() {
    }
    Point(int x, int y) : x(x), y(y) {
    }
};
bool cmp(const Point &u, const Point &v) {
    return u.x < v.x;
}
bool cmp2(const Point &u, const Point &v) {
    return u.y < v.y;
}
int dist(Point &p1, Point &p2) {
    return (p1.x-p2.x)*(p1.x-p2.x) + (p1.y-p2.y)*(p1.y-p2.y);
}
int main() {
    int n;
    scanf("%d",&n);
    vector<Point> a(n);
    for (int i=0; i<n; i++) {
        scanf("%d %d",&a[i].x,&a[i].y);
    }
    sort(a.begin(), a.end(), cmp);
    vector<Point> candidate = {a[0], a[1]};
    int ans = dist(a[0], a[1]);
    for (int i=2; i<n; i++) {
        Point now = a[i];
        for (auto it = candidate.begin(); it!=candidate.end(); ) {
            auto p = *it;
            int x = now.x - p.x;
            if (x*x > ans) {
                it = candidate.erase(it);
            } else {
                it++;
            }
        }
        sort(candidate.begin(), candidate.end(), cmp2);
        int d = (int)sqrt((double)ans)+1;
        auto lower_point = Point(-100000, now.y-d);
        auto upper_point = Point(100000, now.y+d);
        auto lower = lower_bound(candidate.begin(), candidate.end(), lower_point, cmp2);
        auto upper = upper_bound(candidate.begin(), candidate.end(), upper_point, cmp2);
        for (auto it = lower; it != upper; it++) {
            int d = dist(now, *it);
            if (d < ans) {
                ans = d;
            }
        }
        candidate.push_back(now);
    }
    printf("%d\n",ans);
    return 0;
}

ans에는 거리의 제곱이 저장되어 있기 때문에, lower_bound와 upper_bound를 찾기전에 제곱근을 구했습니다. 또, lower_bound를 구할 때, x좌표에는 -100,000을 넣는 이유는 같은 y좌표를 가지는 점이 여러 개일 때, 가능한 x좌표의 값 중 가장 작은 값(-10,000)보다 작기 때문입니다. upper_bound도 마찬가지 입니다.

그럼 이 방법의 시간복잡도는 어떻게 될까요?

이분 탐색을 이용했기 때문에, 뭔가 빠를 것 같이 느껴지지만 실제로는 O(N^2lgN) 입니다. 각각의 점마다 검사해야 하는 점의 최대 개수가 N개 였기 때문에, 이전 방법의 복잡도가 O(N^2) 이었는데, 이번 방법은 정렬을 해야 하기 때문에 N이 아닌 NlgN이 곱해져야 합니다.

이진 트리를 사용해 candidate를 구현하면, 정렬을 사용할 필요 없이 구현할 수 있습니다. 바로 set을 사용하는 것입니다.

set은 삽입, 삭제, 탐색이 모두 O(lgN)이 걸리기 때문에, O(NlgN)이라는 시간으로 가장 가까운 두 점을 구할 수 있습니다.

#include <cstdio>
#include <vector>
#include <set>
#include <algorithm>
using namespace std;
struct Point {
    int x, y;
    Point() {
    }
    Point(int x, int y) : x(x), y(y) {
    }
    bool operator < (const Point &v) const {
        if (y == v.y) {
            return x < v.x;
        } else {
            return y < v.y;
        }
    }
};
bool cmp(const Point &u, const Point &v) {
    return u.x < v.x;
}
int dist(Point p1, Point p2) {
    return (p1.x-p2.x)*(p1.x-p2.x) + (p1.y-p2.y)*(p1.y-p2.y);
}
int main() {
    int n;
    scanf("%d",&n);
    vector<Point> a(n);
    for (int i=0; i<n; i++) {
        scanf("%d %d",&a[i].x,&a[i].y);
    }
    sort(a.begin(), a.end(), cmp);
    set<Point> candidate = {a[0], a[1]};
    int ans = dist(a[0], a[1]);
    for (int i=2; i<n; i++) {
        Point now = a[i];
        for (auto it = candidate.begin(); it!=candidate.end(); ) {
            auto p = *it;
            int x = now.x - p.x;
            if (x*x > ans) {
                it = candidate.erase(it);
            } else {
                it++;
            }
        }
        int d = (int)sqrt((double)ans)+1;
        auto lower_point = Point(-100000, now.y-d);
        auto upper_point = Point(100000, now.y+d);
        auto lower = candidate.lower_bound(lower_point);
        auto upper = candidate.upper_bound(upper_point);
        for (auto it = lower; it != upper; it++) {
            int d = dist(now, *it);
            if (d < ans) {
                ans = d;
            }
        }
        candidate.insert(now);
    }
    printf("%d\n",ans);
    return 0;
}

빨라보이지만 아직도 시간 복잡도는 O(N^2lgN)입니다. 이유는 바로 38~46번줄 때문입니다. candidate에 들어있는 점을 모두 순회하면서 x좌표의 차이를 검사하고 있습니다. 또, set은 y좌표를 기준으로 정렬했기 때문에, 어디부터 어디까지가 x좌표의 거리 차이가 d 이하인지를 알 수 없습니다.

생각해보면, 이미 입력받은 배열을 x좌표순으로 정렬했습니다. set에는 항상 입력받은 배열의 한 구간이 들어가있게 됩니다. 그 구간의 끝점은 항상 i-1이 됩니다. 그럼 시작이 어디인지를 변수 start에 저장하면 됩니다

#include <cstdio>
#include <vector>
#include <set>
#include <algorithm>
using namespace std;
struct Point {
    int x, y;
    Point() {
    }
    Point(int x, int y) : x(x), y(y) {
    }
    bool operator < (const Point &v) const {
        if (y == v.y) {
            return x < v.x;
        } else {
            return y < v.y;
        }
    }
};
bool cmp(const Point &u, const Point &v) {
    return u.x < v.x;
}
int dist(Point p1, Point p2) {
    return (p1.x-p2.x)*(p1.x-p2.x) + (p1.y-p2.y)*(p1.y-p2.y);
}
int main() {
    int n;
    scanf("%d",&n);
    vector<Point> a(n);
    for (int i=0; i<n; i++) {
        scanf("%d %d",&a[i].x,&a[i].y);
    }
    sort(a.begin(), a.end(), cmp);
    set<Point> candidate = {a[0], a[1]};
    int ans = dist(a[0], a[1]);
    int start = 0;
    for (int i=2; i<n; i++) {
        Point now = a[i];
        while (start < i) {
            auto p = a[start];
            int x = now.x - p.x;
            if (x*x > ans) {
                candidate.erase(p);
                start += 1;
            } else {
                break;
            }
        }
        int d = (int)sqrt((double)ans)+1;
        auto lower_point = Point(-100000, now.y-d);
        auto upper_point = Point(100000, now.y+d);
        auto lower = candidate.lower_bound(lower_point);
        auto upper = candidate.upper_bound(upper_point);
        for (auto it = lower; it != upper; it++) {
            int d = dist(now, *it);
            if (d < ans) {
                ans = d;
            }
        }
        candidate.insert(now);
    }
    printf("%d\n",ans);
    return 0;
}