8704번 - Trójmiasto 다국어

W Bajtocji jest n miast, których położenie możemy przedstawić w postaci punktów na płaszczyźnie o całkowitych współrzędnych. Odległość między dwoma miastami o współrzędnych (x₁, y₁) i (x₂, y₂) jest określona w standardowy sposób: √((x₂ - x₁)² + (y₂ - y₁)²).

Król Bajtocji, Bajtazar, chce wyznaczyć trzy miasta, które połączy i zamieni w Trójmiasto (wzorem pewnego egzotycznego królestwa, w którym w Trójmieście odbywają się finały tamtejszej OI oraz rozmaitych międzynarodowych zawodów programistycznych). Bajtazar postanowił wybrać takie trzy miasta, dla których suma odległości pomiędzy każdymi dwoma z nich jest minimalna.

Pierwszy wiersz standardowego wejścia zawiera jedną liczbę całkowitą n (3 ≤ n ≤ 10⁶) oznaczającą liczbę miast w Bajtocji. Miasta są ponumerowane od 1 do n. W kolejnych n wierszach znajdują się po dwie liczby całkowite x_i i y_i (0 ≤ x_i, y_i ≤ 10⁹) oddzielone pojedynczym odstępem, oznaczające współrzędne i-tego wierzchołka miasta.

Pierwszy wiersz standardowego wyjścia powinien zawierać jedną liczbę, równą minimalnej sumie odległości pomiędzy miastami wybranego Trójmiasta, zapisaną z dokładnością do dwóch miejsc po przecinku.

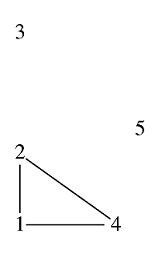
Bajtazar wybierze miasta: 1, 2 i 4.